The cause of the complication is well known - it is called the "noise". Noise is in general some unwanted energy that leads to fluctuations in analog values that we measure, for example in measured voltage or current, but also in any other electrical and non-electrical physical value imaginable. This noisy energy might be added both externally (from the surrounding environment) and internally (by the measurement device itself) and is always unpredictable by its nature - no one can predict its future value by knowing its present value (no, not even the Allmighty). Should the opposite be truth, one could simply subtract the predicted noise from the raw readout producing the super-precise measurement. But in reality we are bound to swallow both sweet and bitter pill at the same time.

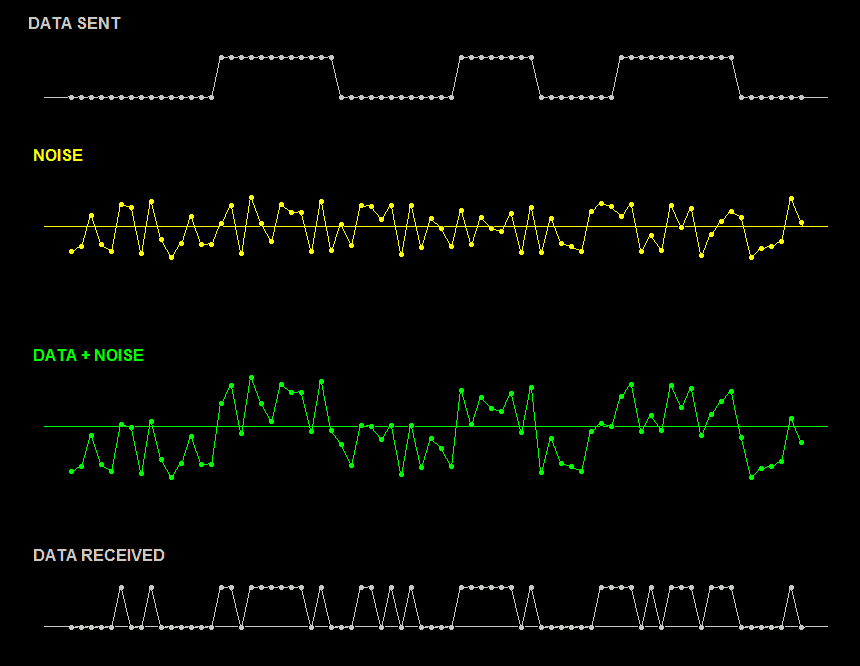
If you red the previous paragraph carefully, you noticed the word "analog" in it. But aren’t we discussing digital electronics here? Well, yes but the truth is that what we call digital is in essence simply analog divided artificially (i.e. by convention) into the well defined bands to which we attach digital state markings. For various technologies conventions vary, for example in +5Vcc TTL circuits every voltage lower than +0.5V is considered "0", while every other is considered "1". In CMOS world the threshold is approximately 1/2V_dd, and in this case +V_dd is between 3V and 15V. But unavoidable truth is that behind every digital gate lurks a microscopic leprechaun with a classical analog voltmeter in its hands; every voltage even the tiniest amount higher than the prescribed threshold it pronounces "1", every other "0".

Because outputs of digital gates are guaranteed to be either "0" or "1" (i.e. either 0V or +V_cc), noise cannot change their amplitude. But what sufficiently strong noise can do is to introduce alterations that did not exist in the original signal. This can be highly dangerous as it can easily lead to a completely false operation of the device. Such added pulses are easy to observe in the diagram above. In less severe cases, noise introduces "jitter" in digital signals, which is the uncertainty in pulse edge position (timing), which might or might not be as destructive to digital systems but is certainly not desirable.

A typical and effective solution to the problem is introducing two thresholds into the decision making process instead of just one, and that is what is commonly designated by the term "Schmidt triggering". Some input voltage is assumed to be in logic state "1" if it became higher than the higher of the two thresholds, but it then has to become lower than the lower threshold to be pronounced "0" again. This way, a small amount of random noise has less chance to confuse the leprechaun should the absolute value of analog input voltage float anywhere between the two thresholds.

This technique works very well in purposely built hardware digital circuits, but in the world of embedded programming we sometimes simply don't have such hardware at hand. If, for example, we need to sample a digital input pin of a microcontroller but none of them has a Schmidt-like buffer gate built in, then we have to try to simmulate such behaviour in software. Depending on the problem complexity and sensitivity to noise, optimal solutions vary.

This article describes one of the simplest techniques which is the most effective to apply when waiting at a "checkpoint" is being buit into the program, in which case it prevents false triggering. Here is what one can do at almost no cost (in terms of program complexity):

Notice that this approach does not filter the signal in time domain, since rapid variations in signal such as "01010101..." will produce equally varying output. But it does filter out singular bits that differ from the surrounding ones. If for example input sequence looks something like "00001000", output of 2/3 voting routine will be "0" all the time. This way one can prevent pulse noise from interfering and spoiling the decision making process. If we remember that numerous algorithms contain "checkpoints" at which the processing stops and waits for input to change in order to carry on with executing the next step on the course, and that the world is awash in electrical pulse noise, it is easy to estimate the great practical value of this simple trick - it prevents premature initiation of important subroutines. It only remains to figure out an efficient way of embedding it into the program.