Probably the simplest but a fairly effective way of doing this is to design a timed sequence of consecutive reads of each input pin, so that the software decides that the state of the input has changed only if it remained inverted (with respect to its previous state) for a certain number of unit time intervals. Such simple algorithm is easy to understand and can be implemented in an unlimited number of ways. The only problem with this approach is that, if done naively and for a high number of input lines, it may easily waste an unnecessarily large amount of processor resources.

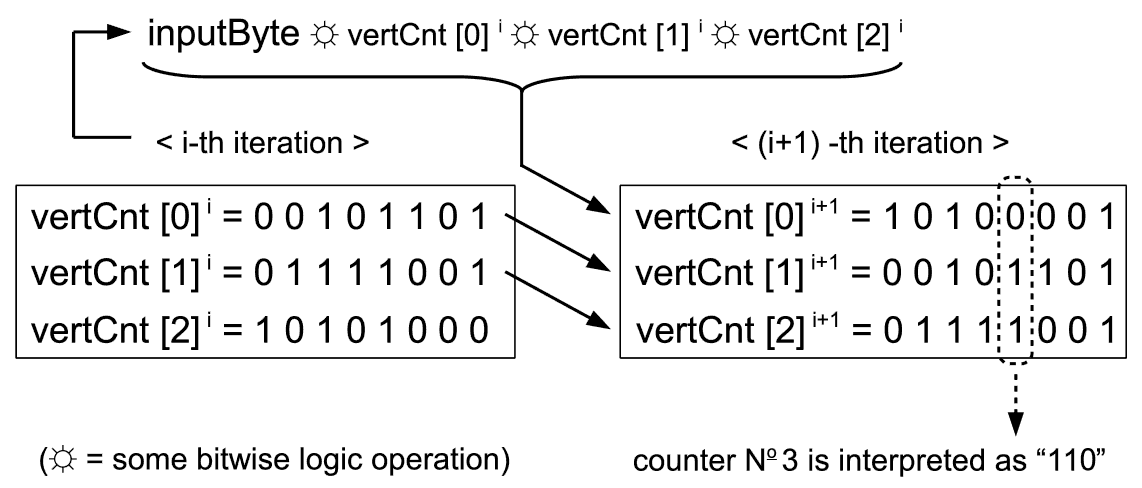
One of the most elegant solutions to the problem is colloquially known under the term “vertical counters”. The idea is to use bits in a single binary variable in such a way so that each bit position represents the current state of a dedicated input line (such bits we usually call ”flags“). If a programmer then forms an array of several such variables, so that variable instances represent input line states sampled at consecutive time intervals, he or she can use bitwise binary logic algebra to do the low pass filtering - in parallel over all bit positions at once. As it is well known, bitwise operations are the fastest commands that can be issued to a processor, since any processor ever made posesses a dedicated hardware that executes them in a single step. The next diagram explains the origin of the attribute “vertical” in vertical counter phrase.

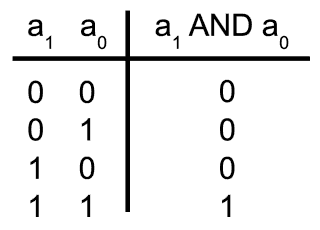
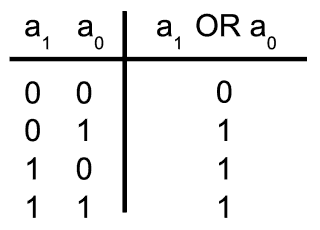
One of the simplest forms of vertical debouncing that comes to mind is a single AND logic function preformed on two consecutive binary variables - only if both bits at a certain bit position are equal to 1, the output at that bit position is read as 1. That could help in preventing false detections of key presses, but the function is far too simple and doesn’t really suit our needs. Firstly, the interval of sampled consecutive key states is too short, and secondly the output result that the AND function produces is highly unsymmetrical; although it would wait a single unit of time before it announced a key press (logic 1), it would get back to 0 as soon as the key reads 0 again. If we remember that the very reason for incorporating a debouncing routine into the program is preventing such rapid changes in filtered key readout, we can start seeking a better candidate binary function. Following the similar reasoning, we easily conclude that none of the binary functions with only two consecutively sampled input binary states is able to do the trick.

Well, let’s then try something a bit more complicated. Let’s first construct the ideal debouncing function having in mind only its filtering effect and then try to synthesize it using a few basic binary functions that are available in microprocessor repertoire. So, what is the ideal output response of the function we seek? If we take the current state of a filtered output bit (in the variable yⁱ_out, where ”i“ denotes the time interval to which it relates), it shall become inverted in the refreshed output variable instance (yⁱ⁺¹_out) only if all corresponding bits at the same bit position in variables from the sample array have got inverted state. The next table illustrates this more clearly. Note that only the states of a single bit position (single input line) are depicted, but with all 16 possible logic combinations those four bits can aquire over three unit time steps. The equivalent table can be drawn for each bit position in input and output vectors.

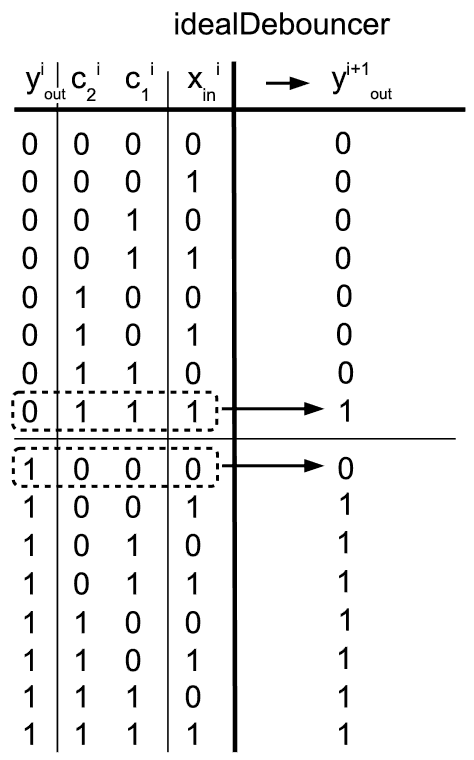
As can be observed, if for example the current state (in the output variable yⁱ_out) of a certain bit is 0, it can become 1 in the next output rendition (yⁱ⁺¹_out) only if both corresponding bits in raw input vectors (cⁱ₁ and cⁱ₂) have become logic 1, and the newly sampled input bit xⁱ_in is also 1. Therefore, the filtering function requires that the input key line is held long enough without bouncing in logic 1 state in order to accept it as a new output logic value. We can apply the same reasoning to the inverse case i.e. if the current filtered output bit yⁱ_out is 1, it can flip to 0 only if both corresponding bits in cⁱ₁ and cⁱ₂ have become 0, and input xⁱ_in also reads 0. This symmetric response is highly desirable in input key filtering as it suppresses uncertainties both when user presses and releases the key.